Kiek kartų fantastiniame kine matėte sceną, kai herojus išsitraukia paskutinę sekundę blasterį ir nušauna priešą? Arba meistriškai apsuka savo kosminį laivą ir nukauna jį persekiojančią blogiečių flotiliją? Be lazerio spindulio neįsivaizduojama jokia dabarties moksline fantastika. Ką kalbėt apie ikoniškus Žvaigždžių karus, kur Lukas meistriškai lazeriu nukauna Mirties žvaigždę?

Ar taps tai kada realybė? Ar mūsų ateities kartos kariaus šviesos spinduliais? Ir nors fantastikos kūrėjai skausmingai melagingai vaizduoja lazerio spindulį (labas rytas G. Lucas, fizikai sako, lazerio spindulį vakuume pamatai du kartus gyvenime – pirmą kartą viena akimi, kitą karta – kita), ar jie pataiko? Ar teisingai numato ateities karų eiga? Pasinagrinėkime!

Mes esame įpratę naudotis žibintuvėliu – lemputė viduryje paraboloidinio veidrodžio. Šio principu veikia beveik visos mūsų kryptingos apšvietimo sistemos – būk tai gatvės žibintas arba mašinos šviesos. Mes galime įsitikinti, kad apšvietimas veikia, kai atsiduriame prasto matomumo sąlygose. Be šviesos mes akli ir nieko aplink nematome, o vat įjungę mašinos lempą – mes lyg įgijame akis. Panašios į rūką aplinkos yra labiausiai tinkamos mums stebėti šviesos elgesį. Taip yra todėl, kad šviesa keliauja tiesiai. Jei jos kelyje nėra kliūčių – mes niekada jos nepamatysime, ji nubėgs į begalybę. Jei šviesos kelyje pastatome kliūtį, ji atsispindės nuo jos ir jei atspindėtos kelyje bus akis, mes ją pamatysime. Rūke labai daug vandens lašų, nuo kurių šviesa sklaidosi. Šią išsklaidyta šviesą mes ir matome, kada įjungiame lempas. Grubiai tariant, mes visada matome objektus (rūko lašus), nes mus pasiekia su jais sąveikavusi lempos šviesa.

Lazeris yra kitoks padaras, todėl ir lazerinė šviesa skiriasi nuo paprastos lemputės-Saulės šviesos. Fizikai sako, kad kasdienė šviesa yra nekoherentinė, o lazerio šviesa – koherentinė. Koherentinė šviesa gerokai pavojingesnė, nes ji galingesnė ir turi kitokias savybes negu paprastoji. Jei paprastai šviesai pamatyti mums daug proto nereikia – paimi ir pažiūri, ar šviečia žibintuvėlis? Fizikai sako, kad lazerio šviesa pamatai akimis tik du kartus gyvenime. Pradžioje lazeris išdeginą vieną akį, po to – antrą.

Nežiūrint į tai, kad lazeris toks pavojingas, jis skleidžia šviesą, kuri yra ir panaši į paprastos lempos šviesą. Dūmai ir rūkas labiausiai tinka tam, kad mes pamatytume lazerio spindulį. Šitoje vietoje noriu skaitytojui užduoti klausimą: O kur vyksta fantastiniuose kinuose lazeriniai mūšiai? Kosmose? Ar yra kosmose dūmų arba rūko? Sakote nelabai? Tada klausimas, o kaip mes matome tada blasterio spindulį, kurį šauna filmo herojus iš savo laivo? Prisiminkime, tuščioje erdvėje lazeriui nėra nuo ko atsispindėti, tad mes negalime matyti kur ir kaip keliauja spindulys!

Tačiau didžiausia mano matyta kvailystė kino istorijoje yra filmai, kur gerojus išvengia lazerinio šūvio pasilenkdamas arba užsidengdamas nuo blasterio. Paklausyte kodėl? Agi todėl, kad šviesa keliauja greičiausiu įmanomu greičiu pasaulyje. Kaip tu gali pamatyti lazerio spindulį anksčiau negu jis atkeliavo? Kas juda greičiau už lazerį? Tiek to, nekalbu apie tai, kad neįmanoma pamatyti realų lazerio spindulį, jei jis netaiko į akį. Bet greičiau už šviesą pamatyt ir… „sureaguoti”! Čia jau tikra fantastika! Ateities lazeriniai mūšiai bus blankūs ir nuobodūs, susitaikykime.

Lazerio šviesa būna įvairi. Dažniausiai, kai spindulio kelyje pastatome prietaisą, kuris išmatuoja lazerio spindulį, mes gauname kokį nors profilį. Nuobodžiausias ir dažniausiai sutinkamas yra Gauso pluoštas. Tai tiesiog lazerinė pointerio dėmelė. Jos pjūvis yra varpo formos ir apsirašo Gauso funkcija su kvadratu nuo atstumo argumente. Svarbiausias tokio pluošto parametras yra pluošto matmuo – spindulys arba diametras. Jei nusiperkate lazerį, pirma ką pamatysite jį įjungus – tokią vat Gauso dėmė.

Kokia pagrindinė problema su kuria susiduria optikai? Gauso lazerinis spindulys yra šviesa. Šviesa plinta. Gauso pluoštelis būna mažas tik šalia lazerio, pamatavus spindulį tolėliau, jis padidės. Fizikai sako, Gausas difragavo. Difrakcija yra pagrindinė informacijos perdavimo laisvoje erdvėje rykštė. Siauriausia Gauso vieta yra vadinama pluošto sąsmauka. Jei aš nupaišysiu, kaip į abi puses tolstant nuo sąsmaukos keičiasi matmuo, aš pamatysiu, kad šalia sąsmaukos pluošto matmuo keičiasi nežymiai bet toliau matmenys auga tiesiškai. Dėsnis pagal kurį tai vyksta yra w = lz/(πw₀). Čia l yra bangos ilgis, z yra atstumas nuo sąsmaukos, w₀ yra matmuo sąsmaukoje, na o π yra π. Turime bėda, kuo mažesnis pluoštas sąsmaukoje, tuo jis labiau plinta.

Galite paklausti, kodėl tai yra bėda? Lazeris yra galia. Kuomet mes perkame galingą lazerį ir norime ką nors nušauti, mes perkame galią, kuri sugeba tai padaryti. Jei pluoštas plinta, jam galioja energijos tvermės dėsnis ir galia tenkantį ploto vienetui mažėja. Grubiai tariant, už kelių metrų mes ne tai kad nenušausime nieko, mums nepakaks apšvietimo antraštei perskaityti. Visa galia yra sukaupta sąsmaukos srityje. Tai reiškia, kad taikinys turi būti sąsmaukoje. Kitaip amen „Star wars”! Mirties žvaigždė sunaikino sukilėlių bazę…

Bet apie kokius dydžius mes kalbame? Galingiausias 10 PW lazeris pasaulyje turi bangos ilgį apie 820 nm ir pluošto diametrą apie 1 mm. Sustatė skaičius gauname sąsmauką apie 3.83 metro. Ne koks ginklas, sakote, jei šauna vos 3 metrus? Pagrindinė kaltininkė čia yra fizika. Vienetiniu egzemplioriumi egzistuojantis lazerinis ginklas šauna geriausiu atveju kilometro atstumu!

Sąsmaukos dydis w0	Bangos ilgis 0.633 µm	Bangos ilgis 10.6 µm
.225 cm	0.045 km	0.003 km
2.25 cm	5 km	0.3 km
22.5 cm	500 km	30 km

Lazerių pramonėje galingi yra CO2 lazeriai, kurių bangos ilgis yra 10.6 mikrometrų. Paėmę realistiškus pluoštų matmenys gauname, kad jų sąsmaukų ilgiai yra gerokai mažesni nei regimos srities (silpnesnių) lazerio. Akivaizdu, kad lazerinis ginklas toli nešaudys. Tarkime, jei galingiausio lazerio dėmę sąsmaukoje padarytume 10 cm dydžio, Mėnulio paviršiuje jos dydis būtų arti kilometro! Jei taikinys yra metro dydžio, iš 10 PW (apie 10^16 W) liks 100 MW galia. Ne kas, pasakysiu. Ypač atsižvelgus, kad čia femtosekundinė sistema.

Kaip matote, difrakcija yra rimta rykštė. Viskas tampa liūdniau, jei paskaičiuojame lazerio spindulį dydį ir galia kokioje mums artimiausioje Saulės sistemoje, Esu rašęs apie fotonų fregatus. Jei girdėjote apie projektą Starshot – difrakcija yra rimtas iššūkis jam, nes per ją mes išbarstysime visą lazerių galią per tarpžvaigždinį atstumą tarp mūsų ir žvaigždės, kur žadame keliauti. Ir čia geras klausimas, ar galime mes ką padaryti?

Atsakymas yra galime! Ir šis atsakymas man tuo malonesnis, nes čia yra lietuvių pėdsako – VU Lazerinių tyrimų centro ir VU FF Kvantinės elektronikos katedros kolektyvas žino kaip suvaldyti difrakciją! Aš jau minėjau, kad lazerius į Lietuvą atvėdė Algis Piskarskas. Šio žmogaus dėka lietuvių lazeristai išmoko pažaboti ir difrakciją!

Kaip mes pavadinsime lazerio pluoštą, kuris nedifraguoja? Daug išmonės nereikia, fizikai juos pavadino nedifraguojančiais. Ką reiškia fizikui sakinys: „Lazerio pluoštas nedifraguoja”? Išvertus į žmonių kalbą tai reikštų, kad lazerio šviesa nekinta, kuomet mes ją stebime toliau ir toliau nuo lazerio. Tokios šviesos matmenys ir struktūra nesikeičia lazerio spinduliui sklindant tolyn. Valio, valio, valio! Pašaudysim visgi blasteriais?! Ne taip spėriai, pasiaiškinkime.

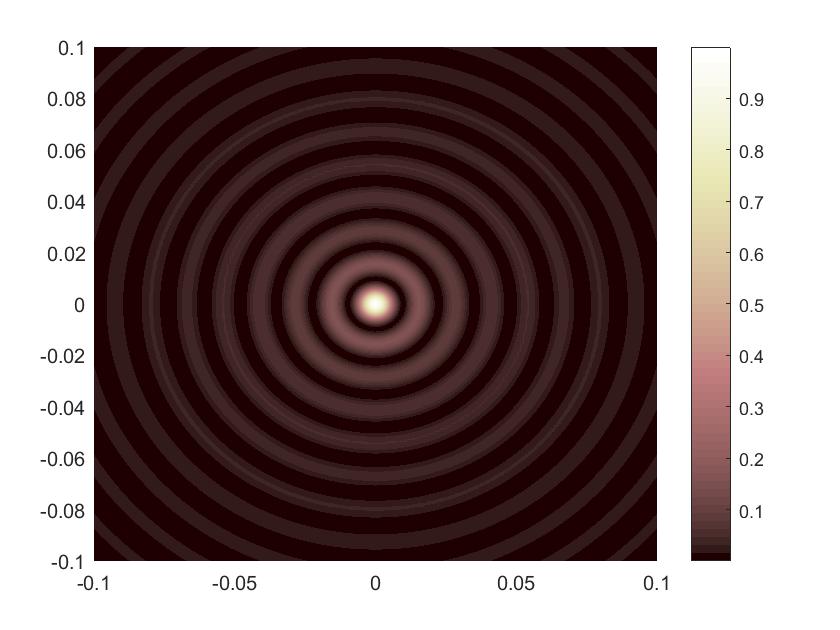
Populiariausias optikoje nedifraguojantis pluoštas yra Beselio pluoštas. Jis atrodo kitaip negu Gauso pluoštelis, jame stebime centre varpo formos piką, tačiau aplinkui šį piką matome ir koncentrinę sistemą silpnėjančiu žiedų. Tai yra kaina, kurią tenka sumokėti sukovojus su šviesos difrakcija.

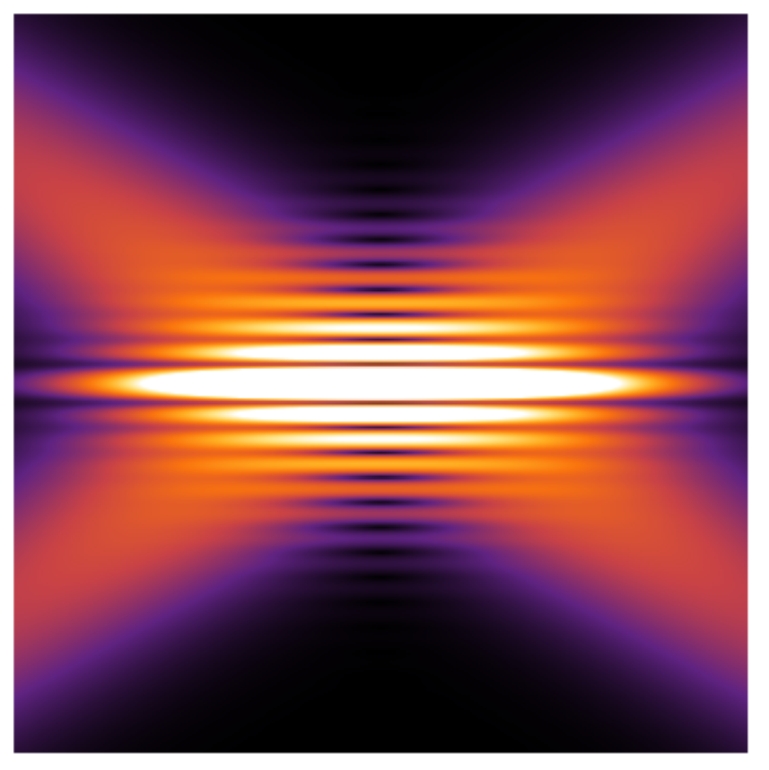
Dar įdomiau tampa, kada pradedame žiūrėti į sąsmauką – mes nerandame nieko panašaus į Gauso pluoštą. Vietoje to mes matome ryškią centrinę smailę, kurios forma yra pastovi – ji kaip adata. Adatos forma mums išduoda, kad pluoštas neplinta – pjūviai adatos yra pastovaus dydžio. Tai pat stebima X-pavidalo raidę fone ir žiedų pjūvius, kurie atrodo paveiksliuke lyg į kraštus silpnėjanti gardelė. Tikrai įdomiai atrodo! Ypač jei visą ligšiolinį gyvenimą vien tik į Gausus težiūrėjai!

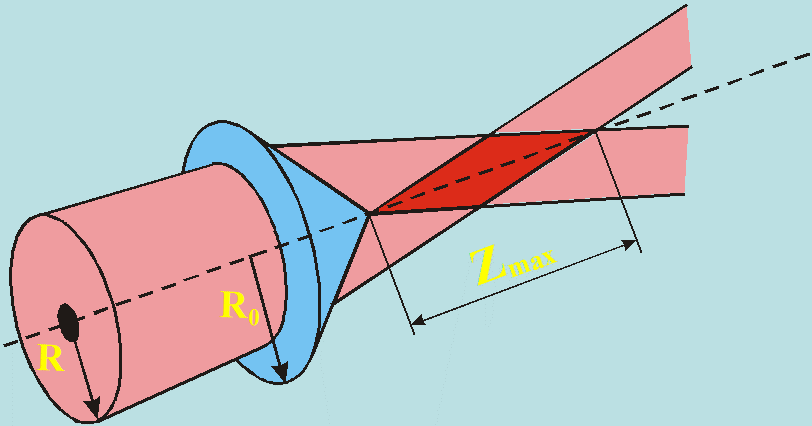
Taip yra dėl to, kad Beselio pluoštas fokusuojamas kitokiu lęšiu. Gauso pluoštą mes pagaminame paprastu lęšiu. Daug proto čia nereikia – paimk gerą lęšį ir jo židinyje bus Gauso pluošto sąsmauka. Beselio pluoštas yra kitoks padaras – jį mes pagaminame paėmė ne lęšį, o prizmę! Ir ne šiap sau paprastą, o specifinę – kūginę prizmę. Jos dar vadinamos protingų žmonių „aksikonais”.

Pažvelgę į fokusavimo schemą patyrę fizikai iš karto pasakytų priežastį, kodėl tokie pluoštai nedifraguoja – šviesos interferenciją. Esu jau minėjęs, kas tai yra. Jei kas galite paskaityti, tuo pačiu gal ir kaleidoskopas gausis.

Kūgis padalina krentančią šviesą į dvi dalis – viena keliauja iš viršaus į apačią, kita – iš apačios į viršų. Kur jos susikerta, šviesa interferuoja ir gauname Beselio pluoštą! Interferencija padeda mums sukovoti su žalinga difrakcija. Geriausia, jog atstumas Z kuriame mes galime padaryti lazerio spindulį atspariu difrakcijai priklauso nuo dvejų dydžiu – kūginės prizmės pagrindo dydžio d ir kampo α, tarp prizmės pagrindo ir trikampio kraštinių Z = d ctg α. Kuo mažesnis kampas α, tuo ilgesnis atstumas. Tuo ilgesnė Beselio zona.

Toks pluoštas yra gera žinia kosmosui – optinė adata leistų mums nutiesti fotonų bėgį iki artimiausios žvaigždės! Mes neišbarstytume energijos ir laivas galėtų nuplaukt šviesos bangomis. Kaip rodo skaičiavimai, praktiškai tai yra sunku, bet įmanoma.

Bet kaip su blasteriais? Jei įsivaizduoju nekantrų skaitytoją. Turiu nuliūdinti – nedifraguojančiais pluoštais mes nepašaudysime. Bet gera žinia yra ta, kad galės iššauti Mirties žvaigždė!!

Jau regiu surauktus veidus: Vėl tu, Orlovai… Matote, reikalas tas, jog dideli atstūmai reikalaus vieno iš dvejų – arba labai mažų kampų kūginėse prizmėse, arba didelių prizmių. Mažai kampai gerai, nes prizmės gali būti mažos, bet blogai, nes tokias prizmės pagaminti bus velniškai sunku. O dideli aksikonai, na patys supraskite, su milžinišku stiklo luitu nepalakstysi, kelnėse nepaslėpsi.

Paskaičiuokime dydžius. Tarkime, norime šauti į Mėnulį. Realistiškas kampas yra apie 0.5 laipsnio, tai bus ctg 0.5 = 114, 6. Tiek kartų mažesnis už atstumą tarp Mėnulio ir šautuvo turi būti aksikono pagrindas tam, kad pluošto diametras nepasikeistų. Jei nežinote tarp Mėnulio ir Žėmės yra 384 000km. Tai duoda 3351 km dydžio aksikoną. Jei šauname tik 3000 km, aksikonas turi būti apie 26 km skersmens. Na, žinote, ne kas, ne kas…

Taigi, palieku jus, atsisveikinu. O išvadą pasidarome patys. Čia namų darbai bus.