Žinote, kas labiausiai mane stebina? Kaip lengvai protingiems bet neturintiems ką veikt žmonėms limpa įvairaus plauko sąmokslo teorijos. Nuo skiepų su mikročipais iki vėžį sukeliančio 5G. Nuo pasaulį užvaldžiusių slaptų draugijų iki sufabrikuoto NASA išsilaipinimo Mėnulyje. Šiame sąraše nereik pamiršt ir žmonių, teigiančių kad planeta yra plokščia. Ir nors esu rašęs bei pasakojęs, jog tokia planetos forma nerealistiška bei prieštarauja fizikos dėsniams, vis teberašo man komentarus čia ir Youtube kanale bei kaltina parsidavimu „driežiažmogėms”. Kaip norėčiau tuos pinigus matyt, patikėkit. Taip būtų šaunu pagaliau gaut ką 🙂

Ir sakykit, kaip paprastai ir aiškiai pasipriešinti tokiems žmonėms? Šiame įraše (kuris galimai bus per ilgas sumuštiniui ir kavai) aprašysiu, kaip galima nesunkiai panaudoti viešai prieinamus duomenys – tokius kaip 2022m. sausio 15 d. Tongos ugnikalnio išsiveržimas, norint gauti tvirtų įrodymų, kad Žemė yra rutulys, ir nustatyti jos perimetrą, naudojant tik paprastą mokyklinę aritmetiką.

Šis mokslinis eksperimentas yra puiki tokio fundamentalaus teiginio iliustracija, tinkanti bet kuriai gamtos mokslus kremtančiai vidurinės mokyklos fizikos klasei. Pabrėžiu, joje naudojami viešai prieinami duomenys, o medžiaga stengiaus pateikti pakankamai paprastai, kad net 12 metų vaikas (arba mokyklą primiršęs suaugęs asmuo) galėtų sekti mano minties eigą. Manau, tokia kelionė į mokslą yra reikšminga kiekvienam mokyklą pamiršusiam ir nuo mokslo atitolusiam žmogui. Be to, visi norintys gali laisvai susirasti savo duomenų rinkinius internete, tačiau galiausiai visi gaus tą patį atsakymą kaip ir mes, beskaitantys šią mano rašliavą.

Šiame įraše paaiškinsiu, kaip patikrinti, ar Žemė yra apytiksliai sfera. Tai dar ne visai 100 procentinis įrodymas, nes jame yra spragų, kurių (pažadu) neslėpsiu, aptarsiu ir, vėliau, visus atvirus klausimus uždarysiu.

Galite paklaust kodėl ugnikalnis? Matot, tokio teorinio pasinagrinėjimo laimei, jie pakankamai dažni, nors tokie galingi ugnikalnių išsiveržimai, kaip Tambora (1815 m.) ar net Krakatau (1883 m.), yra stebimi tik kelis kartus per šimtmetį. Kai jie įvyksta, pasaulis pajunta. Prarastos gyvybės, tušti ir sunaikinti namai bei žmonių pragyvenimo šaltinių dingimas yra staigus ir milžiniškas.

Prieš gerą pusmetį povandeniniame ugnikalnyje Tongos karalystėje įvykusio milžiniško sprogimo kaina taip pat buvo didelė. Kai kurios salyno salos buvo visiškai užtvindytos milžiniškų cunamio bangų, o aukų skaičius buvo didelis.

Sprogimas sukėlė (tiesiogine prasme) kurtinančią garso ir slėgio bangą, tokią galingą, kad ją lengvai galėjo aptikti meteorologinės stotys visame pasaulyje – tiek profesionalios, tiek esančios paprastų žmonių namuose. Tiesą sakant, daugelis tokių meteorologinių stočių bangos praėjimą aptiko net kelis kartus. Nuo termobranduolinių ginklų bandymų eros pradžios iki 1963 m. branduolinių bandymų uždraudimo sutarties, (mano žiniomis) žmonės nėra pastebėję tokios aiškios lengvai susekamos slėgio bangos, kilusios dėl ugnikalnio išsiveržimo.

Skaičiau apie įvertinimus, kad toks sprogimas, susidarantis per akimirką, kuomet vanduo susiliečia su kylančia iš ugnikalnio magma ir virsta garais, turėjo milžinišką galią. Jis prilygo mažiausiai 10 megatonų trotilo sprogimui, beveik tūkstantį kartų stipresnis už žinomas branduolines bombas. Jis yra net palyginamas su didžiausiais kada nors išbandytais termobranduoliniais ginklais.

Kodėl apie tai kalbu? Šeštajame dešimtmetyje paprasti žmonės neturėjo lengvos prieigos prie tikslių meteorologinių stočių duomenų, o ir pačių stočių visame pasaulyje taip pat buvo mažiau. Šiuolaikinių technologijų dėka šis sprogimas, labiau nei bet kuris ankstesnysis, suteikia mums šią unikalią galimybę, tą sidabro kulką prieš plokščiažemininkus, kuria, manau, turėtų pasinaudoti gamtos mokslų mokytojai visame pasaulyje.

Kaip atskirti, ar paviršius, kuriame gyvenate, yra sfera? Lengva, jei ji pakankamai maža, kaip Mažojo princo planeta. Pradedate nuo savo namų ir pradedate eiti bet kuria pasirinkta kryptimi. Tiesiog eikite tiesiai į priekį; galiausiai vėl grįšite namo. Tarkime, užtrukote vieną valandą. Na, o dabar, kai esate namuose, pasirinkite kitą kryptį ir pradėkite eiti tiesiai į priekį tuo pačiu pastoviu tempu, kol vėl grįšite namo. Ši antroji kelionė taip pat turėtų trukti vieną valandą. Kartokite kiek trokštate; kiekviena kelionė pirmyn ir atgal, visomis kryptimis, bus to paties atstumo, o darant prielaidą, kad jūsų ėjimo greitis visada yra toks pat, tai užtruks tiek pat laiko.

Kiekviena iš šių kelionių būtų taku, vadinamu „didžiuoju apskritimu“, kas yra apskritimas, dalijantis sferą į dvi lygias dalis; tai yra ilgiausi apskritimai, kuriuos galite nupiešti ant sferos, ir kiekvienas iš jų yra vienodo ilgio – sferos apskritimo.

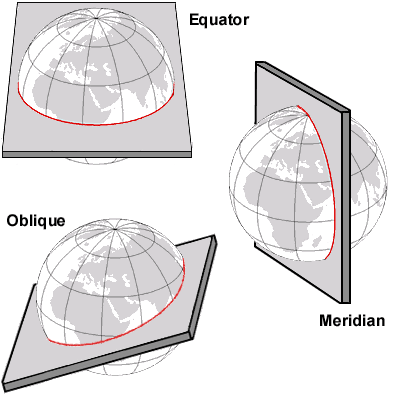
Štai piešinys su trimis iš jų. Garsūs didieji Žemės apskritimai yra pusiaujas ir visos ilgumos linijos (bet ne nulinės platumos linijos, kurios nepadalija pasaulio į lygias puses).

Žinoma, vaikščioti aplink Žemę būtų nepraktiška. Tai ne tik užtruktų per ilgai, bet ir vandenynai trukdytų keliauti. Galite apsvarstyti galimybę skristi lėktuvu, pradedant nuo savo namų ar oro uosto ir keliauti tiesiai į priekį, kol grįšite namo, tačiau išlaidos, politika ir oras jums greičiausiai sutrukdys. Kitos technologijos nėra pažengusios, o be sustojimų į abi puses jos dar ir nepraktiškos.

Tokia galinga sprogimo banga yra mums naudinga nes banga vienu metu skrieja į visas puses. Banga skrieja į šias dideles trukmės ir didelių atstumų keliones aplink pasaulį visomis kryptimis ir mums tai ničnieko nekainuoja – jau nekalbant apie tai, kad ji visiškai apolitiška ir ignoruoja muitines bei pasienius. Banga sklinda į visas puses, sudarydama besiplečiantį ratą. Kad taip ir atsitiko Tongos sprogimo atveju, galima patvirtinti iš slėgio matavimų, atliktų visose pasaulio taškuose. Tačiau taip pat galima bangą pamatyti palydovinėse nuotraukose. Tarkime, ją pamatė palydovas stebėjęs vandens garus planetos atmosferoje.

Tokia banga plis tol, kol pasieks Žemės didijį apskritimą. Tada ji traukiasi sklįsdama toliau, kol susifokusuoja taške, esančiame tiksliai priešingoje Žemės pusėje nuo ugnikalnio. Tada banga praeina pro tą tašką ir vėl pradeda plisti iš jo.

In addition to my recent post about the air pressure wave from the #Tonga eruption side, I provide below a 3D version of the visual explanation why two separate air pressure waveforms could be measured in some earth locations. pic.twitter.com/LmiLQtx3YJ

— StefFun📯 (@StefFun) January 17, 2022

Štai @StefFun vizualizacija, rodanti visą bangos kelionę pirmyn ir atgal. Atkreipkite dėmesį, kad vieną kelionę pirmyn ir atgal sudaro keturi etapai: išsiplėtimas nuo ugnikalnio, susitraukimas į priešingą tašką, vėl išsiplėtimas iš to taško ir susitraukimas atgal į ugnikalnio vietą. Pirmąją pusę galime vadinti „išeinančia“ dalimi, o antrąją – „grįžtančia“ arba „ateinančia“ dalimi. Šis modelis kartojasi vėl ir vėl, kol banga praranda per daug energijos, kad ją būtų galima aptikti.

Iš šių animacijų gali pasirodyti, kad banga apkeliauja pusę Žemės, o paskui atsimuša. Bet iš tikrųjų banga pereina per save! Šioje kelionėje pirmyn ir atgal kiekviena mažytė slėgio bangos dalis kaip Mažasis princas nukeliauja savajį didįjį apskritimą. Taigi ši elgėsį galime panaudoti tam, kad kažką pasakytume apie formą.

Viskas, ką ką tik aprašiau, bus tiesa, jei rėmsiuos dviem prielaidomis:

1. Žemė iš tikrųjų yra beveik sferinė.
2. Smūgio banga tikrai sklinda beveik pastoviu greičiu visomis kryptimis.

Šios dvi prielaidos gali būti patikrintos ir, jei jos (apytiksliai) teisingos, jas galima panaudoti išmatuojant (apytiksliai) Žemės dydį. [Pastaba: mes taip pat darome prielaidą, kad atmosfera yra plona, ​​palyginti su Žemės dydžiu, todėl bangos energija lieka įstrigusi palyginti plonoje srityje virš žemės.]

Štai tokia logika. Jei Žemė yra rutulys, o slėgio banga yra apskritimas, judantis pastoviu greičiu v, tada kiekviena maža slėgio bangos atkarpa apsisuka aplink Žemę „didžiuoju ratu“, kurio ilgis yra sferos perimetras C.
„Kelionės laikas pirmyn ir atgal“, kurį žymėsime „T“, yra vienodas kiekvienai slėgio bangos daliai, kaip parodyta aukščiau esančiame tviteryje, tai gauname T = C / v.

Iš tokio slėgio bangos elgesio padarome išvada: nesvarbu, kurioje Žemės vietoje esate Tongos ugnikalnio atžvilgiu, banga, keliaudama virš jūsų, keliauja aplink Žemę, bendra kelionės trukmės pirmyn atgal yra T. Per tą kelionę viena bangos dalis praeis vieną kartą virš Jūsų, o priešinga bangos dalis, eidama kita kryptimi, praeis virš jūsų grįždama. Todėl šias dvi keliones pirmyn ir atgal pamatysite kaip du įvykius. Kadangi visos bangos dalys juda tuo pačiu greičiu (pagal prielaidą) ir visos nukeliauja tą patį atstumą (pagal prielaidą), turėtumėte gauti tą pačią T reikšmę, nesvarbu, kur gyvenate. Jei galite išmatuoti T ir keturiolikoje kitų šalių turite keturiolika draugų, kurie taip pat gali išmatuoti T analogišku būdu, penkiolika iš jūsų turėtų gauti tą patį atsakymą. Bet kaip mes galime išmatuoti T, kelionės pirmyn ir atgal laiką, sėdėdami namuose?

Ugnikalnis sprogo maždaug 4:15 UTC sausio 15 d. (UTC yra 24 valandų universalus laikas, naudojamas visame pasaulyje, kad esusipainiotumėte dėl laiko juostų, tačiau jis atitinka laiko juostą, kurią naudoja kelios šalys tolimojoje Vakarų Europoje ir Vakarų Afrikoje.) Ši slėgio banga buvo pakankamai stipri, kad sukurti staigius slėgio šuolius ir (arba) slėgio kritimus kiekvieną kartą, kai banga praeina. Juos būtų galima išmatuoti barometrais ant žemės. Daug kur banga buvo pakankamai stipri, atmosfera pakankamai rami, o barometrai pakankamai tikslūs, kad buvo prietaise stebėti keli pikai.

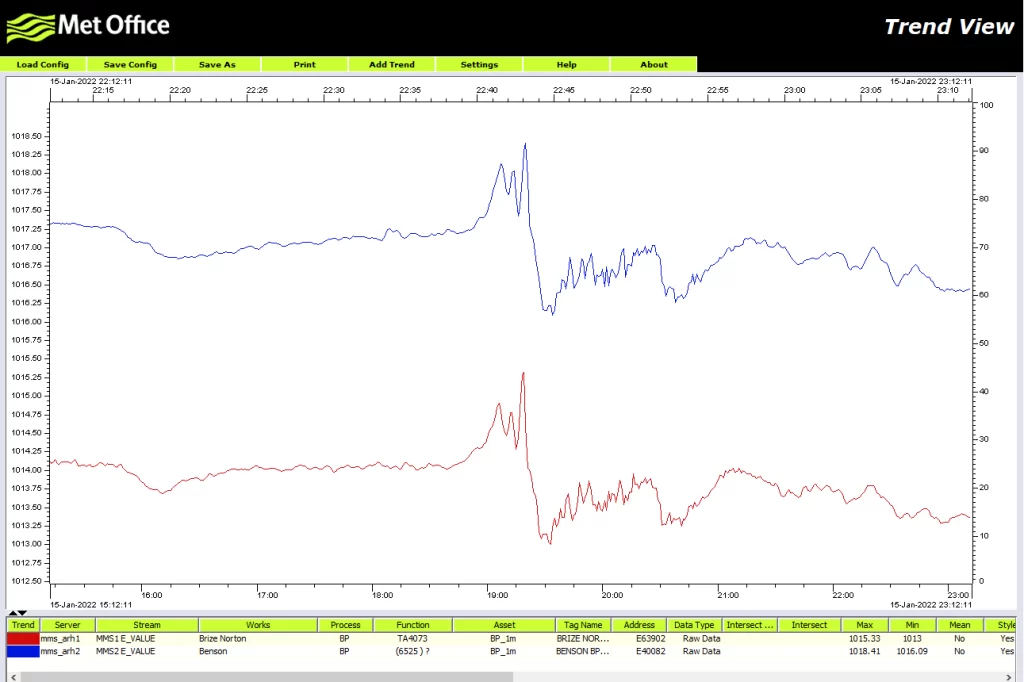
Įsivaizduokime, kad jūs pats turite barometrą, kuris rodo net keturis pikus. Pavadinkime T1 laiką nuo ugnikalnio sprogimo iki pirmojo piko atsiradimo. Panašiai apibrėžsime T2, T3, T4 antrajam, trečiajam ir ketvirtajam pikams. Tada iš šių keturių laiko matavimų galime nustatyti laiką T trimis nepriklausomais metodais ir visi jie turėtų duoti tą patį atsakymą.

Svarbiausias dalykas, kurį reikia atsiminti prieš aiškinant šiuos įvykius, yra tai, kad slėgio banga kiekvieną kelionę pirmyn ir atgal su jumis susitinka du kartus, todėl slėgio šuolį matote du kartus per vieną kelionę pirmyn ir atgal.

Tai reiškia, kad 1 smaigalys prietaise atsiranda dėl bangos smūgio, kai ji iškeliauja pirmuoju reisu pirmyn, o 3 piką sukelia bangos antrasis reisas atgal, todėl juos skiria kelionės pirmyn ir atgal laikas. Kitaip tariant T3 – T1 = T. Panašiai 2 ir 4 šuolius prietaiso ekrane sukelia smūgio banga, kai ji patenka į pirmąjį ir antrąjį reisą, todėl juos taip pat skiria kelionės pirmyn ir atgal laikas T4 – T2 = T. Paskutinis būdas išmatuoti T yra šiek tiek subtilesnis, nors atsakymas labai paprastas. Pasirodo, kad T1 + T2 = T.

Kodėl taip? Svarbiausia, kad greitis v (kurio dar nežinome) yra pastovus. Bangos fronto dalis, kuri skrieja nuo ugnikalnio link jūsų, užtruko T1, kol jus pasiekė, banga įveikė atstumą D1 = T1 v. Tačiau antrąjį piką sukėlė tą bangos dalis, kelionę pradėjusį priešinga kryptimi, nukreipta tolyn nuo jūsų. Ji pasiekė jus nuėjusi ilgą kelią beveik aplink visą Žemę. Tam reikėjo laiko T2, o per tą laiką banga įveikė atstumą D2 = T2 v. Taigi, jei T1 yra laikas, kurio reikia nusklisti atstumą D1, o T2 yra laikas, kurio reikia nusklisti atstumą D2, tada jų suma turi būti laikas, kurio reikia nusklisti atstumą C.

Taigi, jei prietaise stebite keturis pikus, gaunate tris būdus išmatuoti T, kurie turėtų sutapti. Žinoma, jei smūgio banga juda pastoviu greičiu, o linija nuo ugnikalnio iki jūsų sudaro didžiojo apskritimo dalį. Jei matote tris pikus, gausite du matavimus, bet net ir su dviem pikais – be paprastų pasikartojimų – vis tiek gausite vieną T matavimą.

Ką gi, laikas pasiimti kai kuriuos laisvai prieinamus duomenis iš viso pasaulio ir pažiūrėti, kas gaunasi… Pasinaudojau gera svetainė smūgio matavimų laikams. Laikai spėčiau yra 30-90 minučių tikslumu duoti. Tada perskaičiavau juos į laiką, praėjusį nuo ugnikalnio sprogimo, atidžiai atsižvelgdamas į laiko juostas ir konvertuodamas į UTC. Kai kuriais atvejais galėjau nustatyti tik T1 ir T2, bet kartais galėjau gauti T3 ar net T4 . Tada apskaičiavau tiek kelionės pirmyn ir atgal laiko T įverčių, kuriuos galėčiau gauti su dviem, trimis ar keturiais smaigaliais iš kiekvienos vietos. Raginu ieškoti kitų duomenų šaltinių ir patiems tai prasibandyti.

Vietovė	T1	T2	T3	T4	T1 + T2	T3 – T1	T4 – T2
Islandija	1315	2300	4915	5900	35hr 15min	36hr 00min	36hr 00min
Pekinas	0910	2635	4520		35hr 45min	36hr 10min
Olandija	1500	2130	5015	5615	36hr 30min	35hr 15min	34hr 45min
Havajai, USA	0445	3115	3945	6745	36hr 00min	35hr 00min	36hr 30min
New Jersey, USA	1115	2435			35hr 40min
Šveicarija	1545	2100			36hr 45min
Seattle, USA	0830	2745	4415	6345	36hr 15min	35hr 45min	36hr 00min
Pietų Čilė	0845	2805			36hr 50min
Miami, USA	1015	2530	4515		35hr 45min	35hr 00min

Pažymėtina, kad iš šių vietovių, esančių labai skirtingomis kryptimis ir atstumais nuo Tongos gauti duomenys stebėtinai gerai sutampa. Visos mano gautos T reikšmės patenka nuo 34 3/4 valandų iki 36 3/4 valandų, o skirtumas yra mažesnis nei 10%. Mano prasibandymai dažnai buvo dviprasmiški 5 % paklaidos lygyje, nes slėgio bangą dažnai sudarė keli šuoliai ir kritimai, todėl vien iš šio neapibrėžtumo galima tikėtis kelių procentų bangos kelionės laiko nustatyme.

Tokis glaudus T reikšmių sutapimas reiškia, kad abi mūsų pradinės prielaidos – kad Žemė yra sferinė ir kad slėgio banga sklinda pastoviu greičiu – yra teisingos.

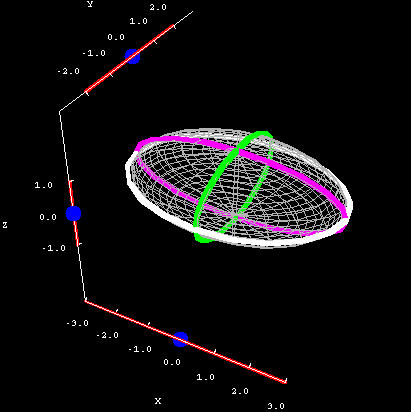
Taigi, gavome visą tai, neišeidamas iš namų ir pasinaudoję viešais duomenemis su 10 procentų tikslumu. Suprantante, pagooglinęs internete, aš nustačiau, jog Žemė yra maždaug sferinė. Ar tai yra visiškas ir galutinis beveik sferinės Žemės įrodymas? Ne. Esu labai arti, bet vis dar matau spragų. Pavyzdžiui, tarkime, kad Žemė atrodo kaip elipsoidas, o ugnikalnis yra tiksliai viename iš elipsoido gale. Tokiu atveju irgi surastume vienodas T reikšmes. Ar suprantate, kodėl?

Yra net plokščios žemės hipotezė, kurios dar visiškai neatmetėme! Kituose įrašuose parodysiu, kaip visam laikui uždaryti klausimą. Skanaus!